Preface

在v2面部模型更新后游戏终于引入了SDF面部阴影；实现上和市面上已有的大部分方案大同小异

本文分享自己在Blender中正确实现该效果的一种思路

注意： 由于个人水平有限错误难免，强烈推荐阅读以下文本作为预备知识：

1. SDF 概述

SDF面部阴影在解决朴素法线/N dot L阈值阴影在极端光照角度表现上的不足以外提供了表现上相当大的自由

具体实现上也相当简洁，以下是HIFI Rush中的应用例

图源：Tango Gameworksのチャレンジが詰まったカートゥーン調リズムアクションゲーム『Hi-Fi RUSH（ハイファイラッシュ）』（1）キャラクター・モー*ション・エフェクト編

美术在（凭不同光照角度于原几何上的）渲染输出为蓝本，手绘出基于角度的阈值图后经某种合成算法后生成一张以亮度映射到光照角度的SDF图像

着色上，SDF可以将点/Fragment渲染的问题转换为物体/Object整体渲染的问题

最后的着色与且仅与光照角度有关（敲黑板），某种程度上来说等效于对法线一致的平面作阴影

合成上，有 Valve 在 SIGGRAPH 2007 上做的技术分享和相当多教程会介绍的8-points Signed Sequential Euclidean Distance Transform/8SSEDT
在之后的文章中将会对这两者进行更深入的实现和剖析

当然，本篇还是以复现游戏效果为主

2. 游戏内实现

抽出游戏所用的SDF贴图如下

faceSdf

在 Photoshop 中查看阈值，很显然是上文所介绍过的类似模型

回忆我们所需的阈值对应光照角度；接下来马上就会用到（再次敲黑板）

3. Blender 实现

光照角度

从角度出发，考虑单个光向量$l$ —— 如图（来自 RTR4 …当然这里和BRDF并没有直接联系

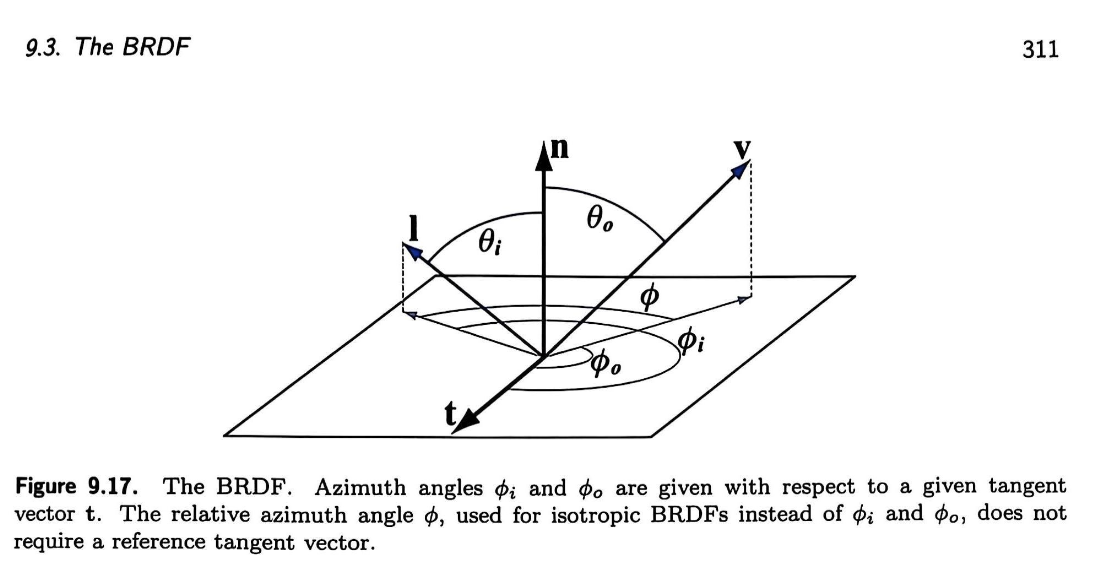
由于对称性很显然只凭$ \mathbf{\hat{n}} \cdot \mathbf{\hat{l}}$ 我们只能获得 $\theta \in [0,90\degree]$的光照角（$<0$ 部分背光故省去）

但引入切向量可以解决该问题！如此将允许我们将光向量放在球面坐标中观察

只看法向量$n$和切向量$t$，不考虑视角$v$

显然有$cos\theta_i = n \cdot l, cos\phi_i = t \cdot l$
回顾之前$\theta$范围，可以注意到$\phi \leq 180\degree$ 对应$b = n \times t$一侧半空间，反之亦然
如次，结合对称性，根据$\phi$就可以轻松得到$[-90\degree,90\degree]$的光照角
公式如下，记$\omega$为最后光照角度 $$ \omega = \theta_i * sgn(sin \phi_i) $$

切空间角度

注：其实这块完全不用写 = = $\theta$角和$N$的关系理应很显然为$cos\theta= \mathbf{L \cdot N}$

接下来介绍使用切空间/$\mathbf{TBN}$表示的方法

首先由上文已知我们已经有了正交基$\mathbf{t,b,n}$($b$为$t,n$叉积），$\mathbf{TBN}$矩阵如下 $$ \mathbf{TBN} = \begin{bmatrix} T_0 & B_0 & N_0 \newline T_1 & B_1 & N_1 \newline T_2 & B_2 & N_2 \end{bmatrix}. $$ 很显然，$\mathbf{TBN}$是个正交矩阵，意味着它的转置等于它的逆 $$ \mathbf{TBN}^\top = \mathbf{TBN}^{-1} = \begin{bmatrix} T_0 & B_0 & N_0 \newline T_1 & B_1 & N_1 \newline T_2 & B_2 & N_2 \end{bmatrix}. $$

接下来做线形空间变换将光照向量$\mathbf{L}$放到切空间中有： $$ \mathbf{L} = [x_0,y_0,z_0]^T = a\mathbf{T}+b\mathbf{B}+c\mathbf{N} $$

$$ \begin{bmatrix} a \newline b \newline c \end{bmatrix} = \mathbf{TBN}^{-1} \begin{bmatrix} x_0 \newline y_0 \newline z_0 \end{bmatrix} = \mathbf{TBN}^\top \begin{bmatrix} x_0 \newline y_0 \newline z_0 \end{bmatrix} $$

$$ \left\lbrace\begin{array}{clcr} a = T_0 x_0 + T_1 y_0 + T_2 z_0 = \mathbf{L \cdot T} \newline b = B_0 x_0 + B_1 y_0 + B_2 z_0 = \mathbf{L \cdot B} \newline c = N_0 x_0 + N_1 y_0 + N_2 z_0 = \mathbf{L \cdot N} \end{array} \right. $$

$L$在$\mathbf{t}$所在平面投影有

$$ \mathbf{L_bn} = b\mathbf{B}+c\mathbf{N} = \mathbf{L} - a\mathbf{T} $$

求$\theta$即为

$$ cos\theta=\mathbf{L_{bn} \cdot N} = \mathbf{L \cdot N} $$

同理易得

$$ cos\phi = \mathbf{L \cdot T} $$

切空间构造

相当多 Blender 中实现 SDF 的教程都作了“着色面法向量就是+Y轴”的假设，如设置 Driver 直接取指向光的 Euler Z作方位角

问题显而易见；接下来介绍一种不作准确度妥协以在 Blender 实现该trick的一种方式

Driver

考虑动画会在骨架上进行，这里考虑直接在骨骼上取法向量

游戏角色模型中一贯都会有一个Head骨骼，后面可以用到；方便期间，后文将使用简化模型进行部分演示

和之前取边缘高光的思路相似，直接取用World Space的Euler XYZ计算骨骼对应的法向量

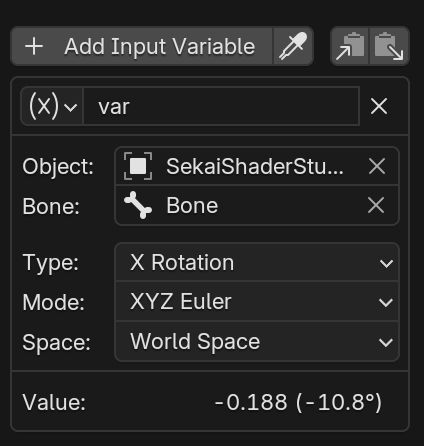
World Space的好处良多，其一就是该值的演算包含动画（FCurve），Constraint和Parenting - 即使对骨骼也是如此

效果如下：

构造正交基

当然，如此我们还没有切向量$t$；幸运的是从法向量构造正交基并非难事

以下代码块均来自参考论文Building an Orthonormal Basis from a 3D Unit Vector Without Normalization - Frisvad, Jeppe Revall

朴素的想法很简单：在离法向量更近的轴上选一个，正交化，做叉乘即得$n,t,b$正交基底

void naive ( const Vec3f & n , Vec3f & b1 , Vec3f & b2 )
{
  // If n is near the x-axis , use the y- axis . Otherwise use the x- axis .
  if(n.x > 0.9 f ) b1 = Vec3f (0.0f , 1.0f , 0.0f );
  else b1 = Vec3f (1.0f , 0.0f , 0.0f );
  b1 -= n* dot (b1 , n ); // Make b1 orthogonal to n
  b1 *= rsqrt ( dot (b1 , b1 )); // Normalize b1
  b2 = cross (n , b1 ); // Construct b2 using a cross product
}

这种做法直觉地符合我们对$t$向量的要求：可以决定光向量在$b = n \times t$哪一侧

而论文中给出的构造方法则相当优美

void frisvad ( const Vec3f & n , Vec3f & b1 , Vec3f & b2 )
{
if(n.z < -0.9999999 f) // Handle the singularity
{
  b1 = Vec3f ( 0.0f , -1.0f , 0.0f );
  b2 = Vec3f ( -1.0f , 0.0f , 0.0f );
  return ;
  }
  const float a = 1.0 f /(1.0 f + n.z );
  const float b = -n.x*n .y*a ;
  b1 = Vec3f (1.0 f - n .x*n. x*a , b , -n .x );
  b2 = Vec3f (b , 1.0 f - n .y*n. y*a , -n .y );
}

可见我们不需要叉乘，不需要归一化也能得到两个额外基底

篇幅（和水平）有限这里不多做介绍，有兴趣还请参考原文理解

接下来在Blender中使用Shader Node实现就很轻松了（注：此处忽略了法线处于z轴分界点情形）

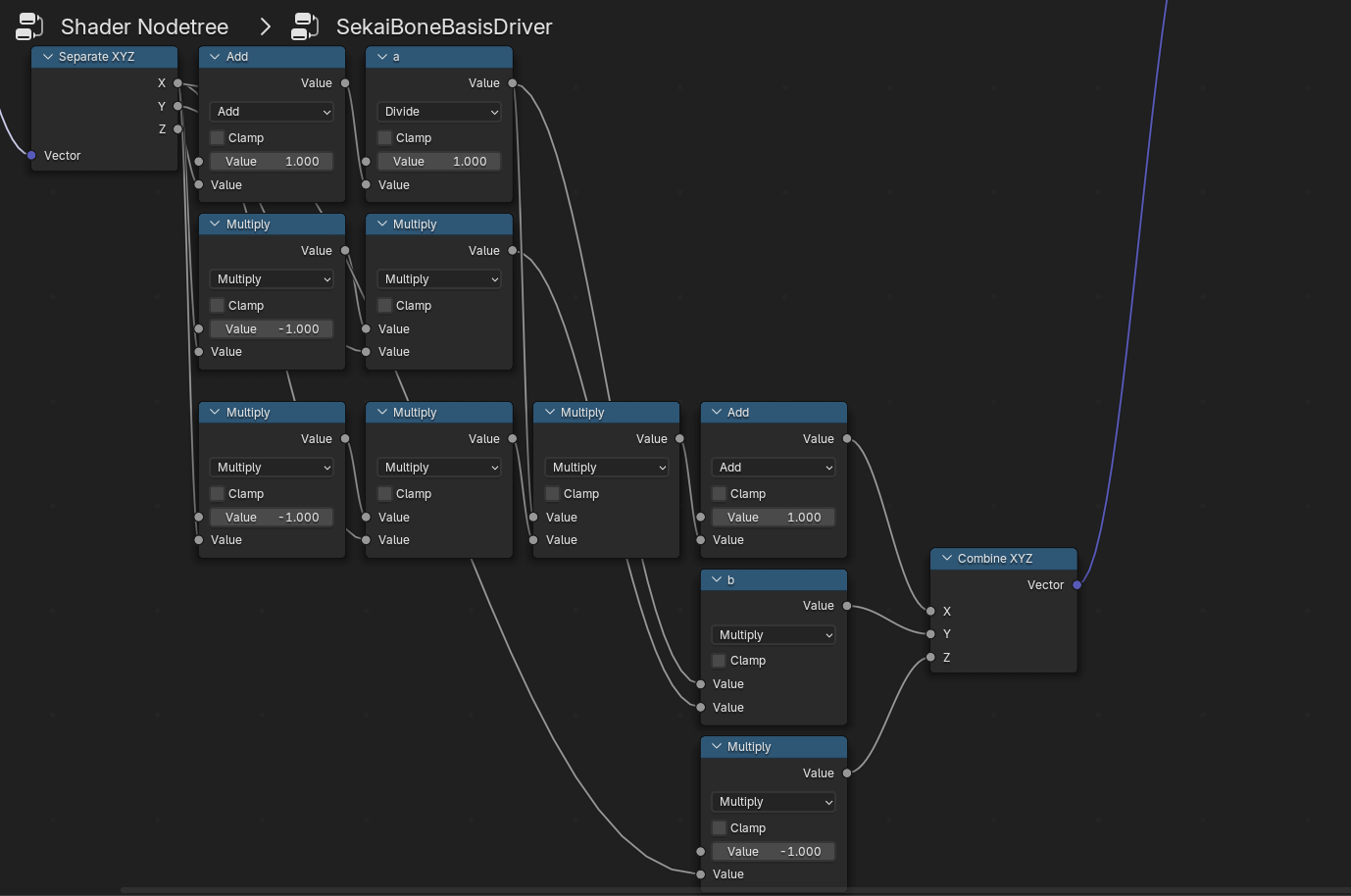
整理实现

利用上文的$cos \phi, cos \theta$，实现轻而易举

素材处理

其一，由于游戏内素材只考虑水平角的光照方案，故计算$\theta$角时有必要丢掉$z$轴计算；否则该角度上带来的角度差只会带来错误
- 带垂直角的方案请参见文首链接，暂不介绍
其二，贴图只包含水平角在$[0,90\degree]$的信息；意味着超过该范围（于$[-90\degree,0]$）需要借用对称性反转
- 由此脸模也需要对称；当然，制作两张SDF贴图就不会有这样的限制

Node如下

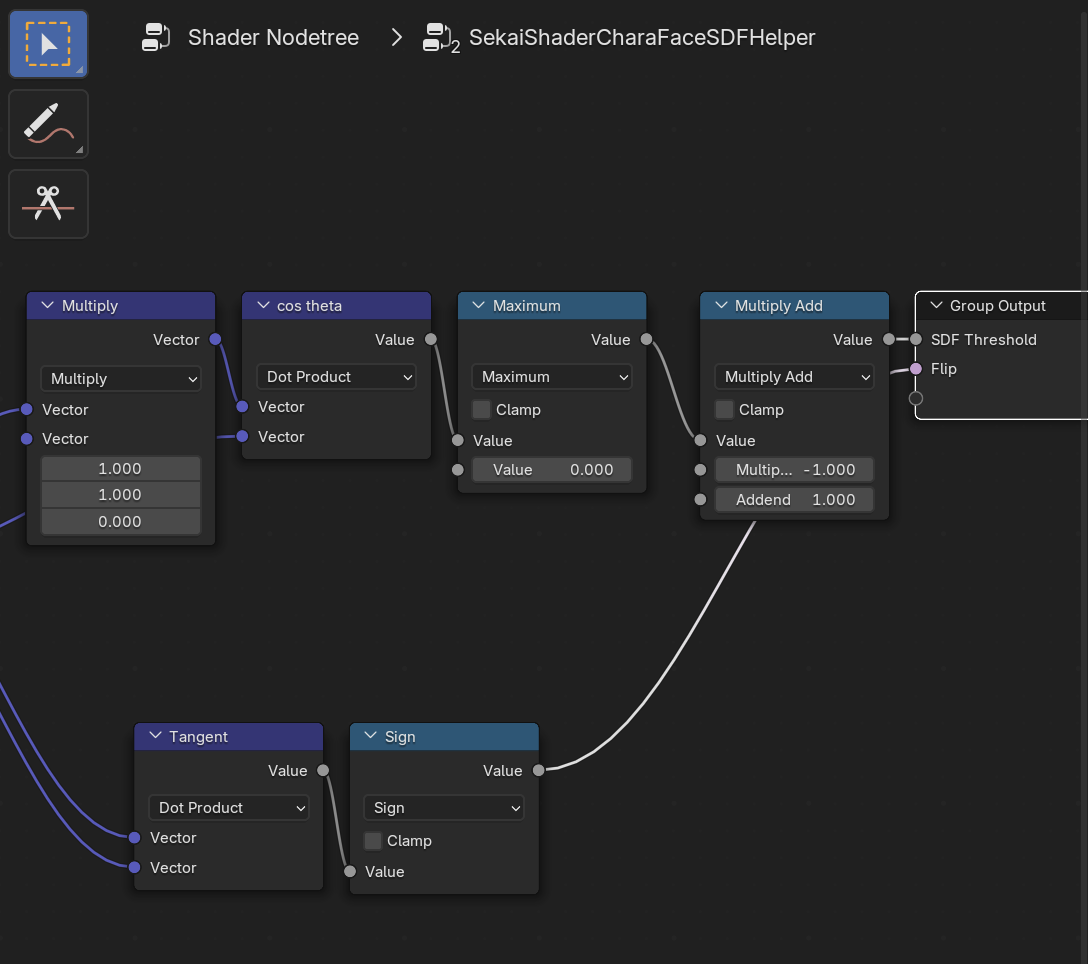
用于反转的Node如下

反转即简单的$u = 1 - u$

最终效果

在动画中实践效果如下;可见阈值光照在骨骼动作上也有正确变化

PSJK Blender卡通渲染管线重现【3】- SDF 面部渲染实现

Preface

1. SDF 概述

2. 游戏内实现

3. Blender 实现