Preface

对网格数据而言，顶点数可以很多很多：如果存储每个顶点的开销能够减少，显然对GPU显存和磁盘存储压力而言是非常好的事情。以下介绍目前Editor内存在的一些量化操作。glTF中的顶点可以有以下属性（参见 Spec）：

NameAccessor Type(s)Component Type(s)Description
POSITIONVEC3floatUnitless XYZ vertex positions
NORMALVEC3floatNormalized XYZ vertex normals
TANGENTVEC4floatXYZW vertex tangents where the XYZ portion is normalized, and the W component is a sign value (-1 or +1) indicating handedness of the tangent basis
TEXCOORD_nVEC2float unsigned byte normalized unsigned short normalizedST texture coordinates
COLOR_nVEC3 VEC4float unsigned byte normalized unsigned short normalizedRGB or RGBA vertex color linear multiplier
JOINTS_nVEC4unsigned byte unsigned shortSee Skinned Mesh Attributes
WEIGHTS_nVEC4float unsigned byte normalized unsigned short normalizedSee Skinned Mesh Attributes

下面为完整精度的顶点struct，足矣表示glTF标准中的任何非蒙皮（不看JOINTS, WEIGHTS）网格（vertex color暂时忽略）。

struct FVertex
{
    float3 position;
    float3 normal;
    float3 tangent;
    float bitangentSign;
    float2 uv;
};
static_assert(sizeof(FVertex) == 48);

FP16 量化

现代GPU基本都有硬件级别的 FP16（半精度）支持。业界包括 Unity 在内在存储顶点数据时也提供了烘焙部分通道（vertices/normals/…）为该精度的选项，实现上这也比较简单。

CPU，或者C++侧对有限精度浮点数的支持一直以来并不友好 - 毕竟硬件级相关指令在AVX512才有。在C++23中才有了语言级别的float16/float64/float128甚至是bfloat16的支持——鉴于某M姓编译器对23标准的支持仍是draft，暂时不考虑升级标准支持这些特性。

当然，手动进行FP32-FP16转化是可能的。全精度和半精度的二进制结构都在IEEE 754中定义了几十年，标准上不存在问题。以下转换实现再次来自meshoptimizer：

union FloatBits
{
    float f;
    unsigned int ui;
};
unsigned short quantizeFP16(float v)
{
    FloatBits u = {v};
    unsigned int ui = u.ui;
    int s = (ui >> 16) & 0x8000;
    int em = ui & 0x7fffffff;
    // bias exponent and round to nearest; 112 is relative exponent bias (127-15)
    int h = (em - (112 << 23) + (1 << 12)) >> 13;
    // underflow: flush to zero; 113 encodes exponent -14
    h = (em < (113 << 23)) ? 0 : h;
    // overflow: infinity; 143 encodes exponent 16
    h = (em >= (143 << 23)) ? 0x7c00 : h;
    // NaN; note that we convert all types of NaN to qNaN
    h = (em > (255 << 23)) ? 0x7e00 : h;
    return static_cast<unsigned short>(s | h);
}
float dequantizeFP16(unsigned short h)
{
    const unsigned int s = static_cast<unsigned int>(h & 0x8000) << 16;
    const int em = h & 0x7fff;
    // bias exponent and pad mantissa with 0; 112 is relative exponent bias (127-15)
    int r = (em + (112 << 10)) << 13;
    // denormal: flush to zero
    r = (em < (1 << 10)) ? 0 : r;
    // infinity/NaN; note that we preserve NaN payload as a byproduct of unifying inf/nan cases
    // 112 is an exponent bias fixup; since we already applied it once, applying it twice converts 31 to 255
    r += (em >= (31 << 10)) ? (112 << 23) : 0;
        FloatBits u;
        u.ui = s | r;
        return u.f;
    }

应用上，我们只对float3 position做FP16存储 - 这是顶点数据中唯一一种分量可取全体实数范围的值。对于其他有界的量，我们可以进行…

定点量化

若值域已知，用定点方式表示浮点数也是很常见的有损压缩技巧——Unity对蒙皮权重就有这样的操作。特别地，对于值域在$[0,1]$ (UNROM) ,$[-1,1]$ (SNORM)的数而言，我们可以直接省去值域本身的存储：毕竟就在名字(“Unsigned Normal”,“Signed Normal”) 里嘛。

这两者实现上非常直觉：$\text{数值}*\text{值域区间}$ 即得到量化后数值，反过来也很简单。实现（及SNORM以UNORM无符号存储变式 [de]quantizeSnormShifted）如下，$N$为量化bit数

inline uint32_t quantizeUnorm(float v, int32_t N)
{
    const auto scale = static_cast<float>((1 << N) - 1);
    v = (v >= 0) ? v : 0;
    v = (v <= 1) ? v : 1;
    return static_cast<int>(v * scale + 0.5f);
}
inline float dequantizeUnorm(int32_t q, int32_t Nbits) { return q / static_cast<float>((1 << Nbits) - 1);}
inline int32_t quantizeSnorm(float v, int32_t N)
{
    const auto scale = static_cast<float>((1 << (N - 1)) - 1);
    float round = (v >= 0 ? 0.5f : -0.5f);
    v = (v >= -1) ? v : -1;
    v = (v <= +1) ? v : +1;
    return static_cast<int>(v * scale + round);
}
inline float dequantizeSnorm(int32_t q, int32_t Nbits) { return q / static_cast<float>((1 << (Nbits - 1)) - 1); }
inline uint32_t quantizeSnormShifted(float v, int32_t Nbits)
{
    return quantizeSnorm(v, Nbits) + (1 << (Nbits - 1));
}
inline float dequantizeSnormShifted(uint32_t q, int32_t Nbits)
{
    return dequantizeSnorm(q - (1 << (Nbits - 1)), Nbits);
}

应用上对于法向量(normal)，切向量(tagent)：他们（规范化为单位向量时）确实可以直接用SNORM表达，你也可以这么做！但是，更高效的法向量存储是存在的，请看下一节。

Tangent Frame 压缩

高效法向量存储是个热门话题：延后（Deferred）渲染流行以来：因有在GBuffer存储法向量的必要，且内存有限，能够高效存储法线/切线/TBN(Tangent-Bitangent-Normal)矩阵做bump map是很值得追求的一个目标。

正如前文所述，对于单位的normal，tagent：定点量化也是一种选择。不过对于单位向量而言，我们的压缩策略是很多的——部分参考Compact Normal Storage for small G-Buffers - Aras Pranckevičius这篇老文章；以下介绍几个比较新且业界有应用的几个压缩方案。

单位向量投影

方案之一的idea来自：规范化的三维单位向量可以投影到某种二维坐标表示。更熟悉地，问题可以描述为：在球坐标系，规范长度为$1$时，就能用仅极角，方位角表示单位长度的所有向量。

参考 Survey of Efficient Representations for Independent Unit Vectors - 2. 3D Unit Vector Representations，我们刚刚描述的正为其中spherical方案。当然，更为巧妙地投影方式也存在：

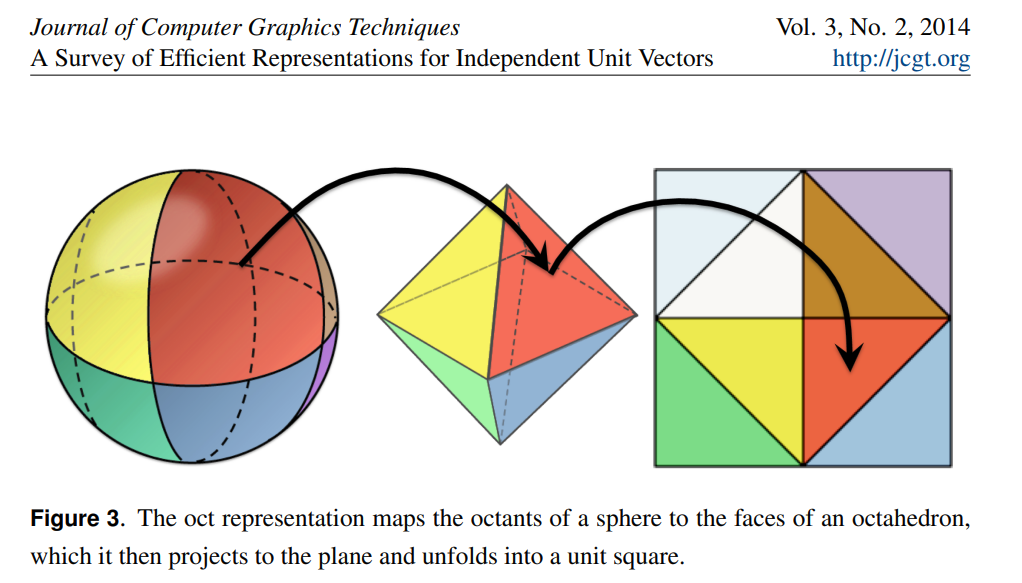
image-20251205084118183

文中的oct方案，也就是八面体，则被认为是"Best overall method"。原理上很优雅，引用原文：

The reason that the mapping is computationally efficient (and elegant) is that it maps the sphere to an octahedron by changing the definition of distance from the $\mathbf{L^2}$ (Euclidean) norm to the $\mathbf{L^1}$ (Manhattan) norm

即为$\mathbb{R^3}$单位圆在$L_1$范数（曼哈顿距离）下的投影。实现如下。可见实现上不需要三角函数——解码时甚至不需要除法！

// Original formulation from: https://jcgt.org/published/0003/02/01/paper.pdf
// R3, L2 to L1 projection on unit sphere
float2 packUnitOctahedralSnorm(float3 v)
{
    // Project the sphere onto the octahedron, and then onto the xy plane
    v /= float3(fabsf(v.x) + fabsf(v.y) + fabsf(v.z));
    // Reflect the folds of the lower hemisphere over the diagonals
    return v.z >= EPS ? v.xy() : (float2(1.0f) - abs(float2(v.yx()))) * sign(float2(v.xy() + EPS));
}
// Original formulation from: https://jcgt.org/published/0003/02/01/paper.pdf
// R3, L1 to L2 projection on unit sphere
float3 unpackUnitOctahedralSnorm(float2 v)
{
    float3 nor = float3(v.xy(), 1.0f - fabsf(v.x) - fabsf(v.y));
    float2 xy = nor.z >= EPS ? v.xy() : (float2(1.0f) - abs(float2(v.yx()))) * sign(float2(v.xy() + EPS));
    return normalize(float3(xy.x, xy.y, nor.z));
}

最后有相关shadertoy演示有限bit数量化后压缩效果：Normals Compression - Octahedron by iq。可见即使在较低量化空间下，视觉效果也是可观的。

四元数存储

不过，如果要做normal/bump mapping的话，完整的TBN/切空间基底是少不了的。我们还需要知道切向量（Tangent）

注意切空间和法线贴图的关系并没有绝对的标准（参见 Tangent Space Normal Maps - Blender Wiki），一个法向量可以对应无穷多的切向量。不过包括 glTF，Blender，Unity，UE在内基本都在用的是 MikkTSpace，大多数法线贴图也是于这里提供的切空间烘焙——同时因为关系非1:1,一般地，拥有法线贴图的网格也的顶点会离线存储这样的切向量以确保正确性——假如有烘焙好的tangent，离线存储是一定要做的。

Bitangent 符号

一个常见trick即为离线存储时，只存储$\mathbf{n}, \mathbf{t}$和一个符号量：应为共面，$\mathbf{b}$即为$\mathbf{n} \mathbf{t}$叉乘，并做这样的翻转。glTF也是这么做的：

NameAccessor Type(s)Component Type(s)Description
POSITIONVEC3floatUnitless XYZ vertex positions
NORMALVEC3floatNormalized XYZ vertex normals
TANGENTVEC4floatXYZW vertex tangents where the XYZ portion is normalized, and the W component is a sign value (-1 or +1) indicating handedness of the tangent basis

假设完整精度直接存储，我们的tangent frame这样需要$4*(3+4)=28$字节。当然上述的投影+量化技巧也值得应用，不过原理上并没有新东西，这里不阐述。

四元数压缩

其实直接间看矩阵形式：我们定义$\mathbf{TBN}$矩阵是个3x3的正交阵——当且仅当$det(M)=1$时，这相当于旋转矩阵，这是可以直接用四元数表示的，在glm中可以直接利用mat3_cast和quat_cast相互转换。

注意： 对于$det(M)=-1$的旋转反射矩阵，四元数是无法表示的，这在bitanget手性不一致（即$\mathbf{n} \mathbf{t} = -\mathbf{b}$）时会如此。接下来我们只对$det(TBN)=1$情况处理，其他情况正交化并以某种方式记录并确保手性即可。

该操作在 Bindless Texturing for Deferred Rendering and Decals - MJP, 压缩tangent frame - KlayGE中都有提及。不过注意，直接存储四元数$(xyzw)$也是很浪费的（$4*4=16$字节！)。不过值得注意的是，单位四元数，即$x^2+y^2+z^2+w^2=1$可以用来表示这里的变换。上面两篇文章也都提到了如何利用该性质$4$字节完成四元数存储的任务。接下来将介绍四元数压缩的一种高精度实现。

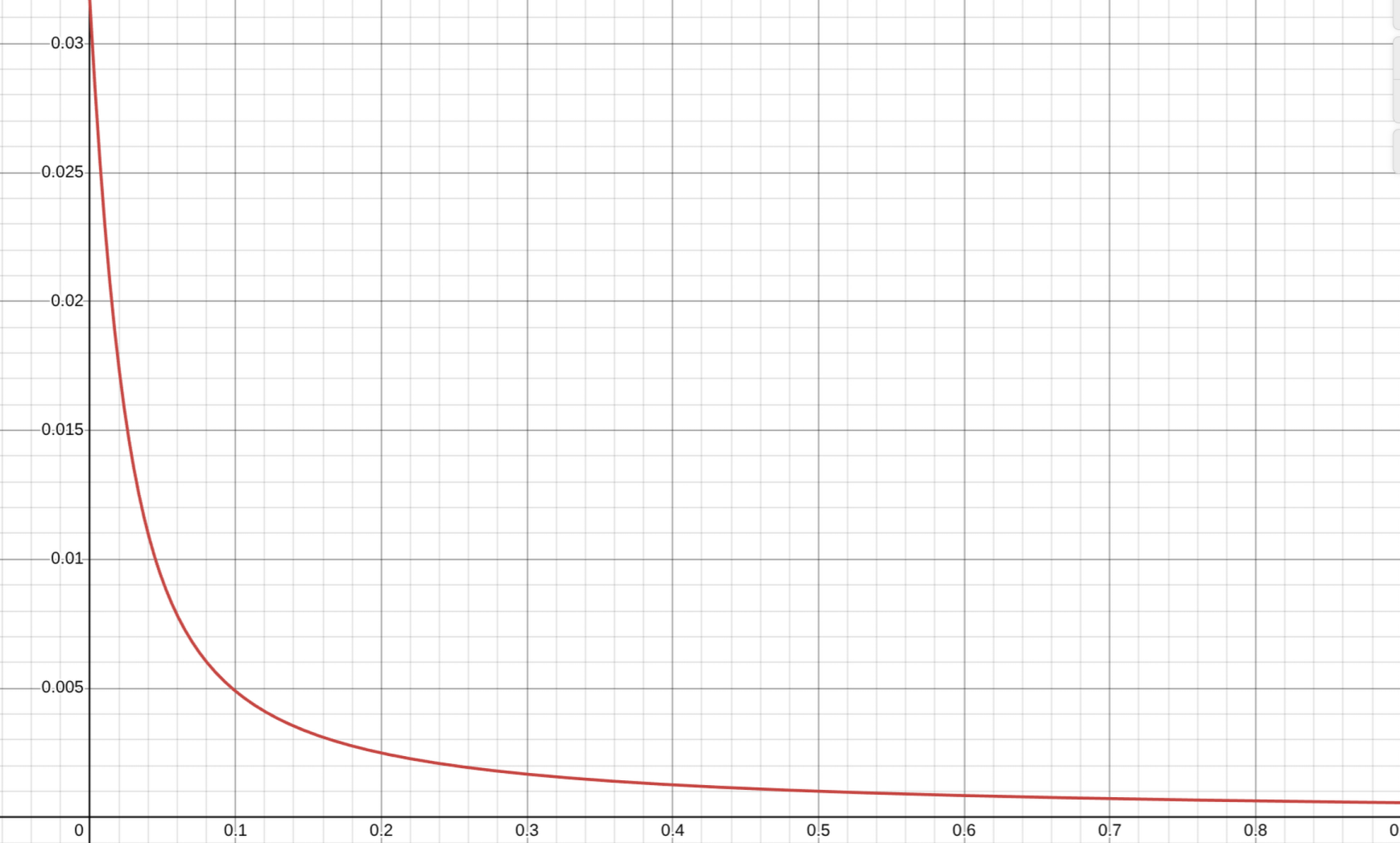
KlayGE直接利用$RGB10A2$格式存储了$x,y,z$部分，最后$A$记录$w = \pm\sqrt{1-x^2-y^2-z^2}$的符号。不过，精度上的优化空间是可循的：MJP文章引用的The BitSquid low level animation system用$A$去记录四个分量中绝对值最大的分量【位置】。原因引用原作者：

…You could use arithmetic encoding to store x, y and z using 10.67 bits per component for the range -1, 1 and this would give you slightly better precision for these values. The problem comes when you want to reconstruct w using sqrt(1-x^2-y^2-z^2) because that function is numerically unstable for small w. Have a look at this graph: https://www.desmos.com/calculator/nfdbj0law4 Below w=0.5 the error starts to become bigger than the error (0.001) in the input values and as we get closer to zero the error becomes a lot bigger (0.03).

文中graph如下，对应$\sqrt{w^{2}+0.001}-w$：可见$w<0.5$之后的计算误差增长非常快。去重构绝对值最大值而非可能最小的$w$即可以避免这种数值误差。

image-20251205163112243

另外，一个实现细节在于：$q=(x,y,z,w)$与$-q=(-x,-y,-z,-w)$表示的是同一个变换。我们可以借此简化之前的$w$意义为四个分量中最大的分量【位置】，包括符号：这建立在若绝对值最大分量为负，则全体取反的基础上。

结合以上信息，以下为四元数压缩的具体实现——参考 TheRealMJP/DeferredTexturing。稍作修改即可适用slang shader。

// Packs quaternion to [UNORM XYZ, 2-bit max index]
inline float4 packQuaternionXYZPositionBit(quat const& q)
{
    float4 Q(q.x, q.y, q.z, q.w);
    float4 absQ(abs(Q.x), abs(Q.y), abs(Q.z), abs(Q.w));
    float absMax = max(max(absQ.x, absQ.y), max(absQ.z, absQ.w));
    uint maxIndex = 0;
    if (absQ[0] == absMax)
        maxIndex = 0;
    if (absQ[1] == absMax)
        maxIndex = 1;
    if (absQ[2] == absMax)
        maxIndex = 2;
    if (absQ[3] == absMax)
        maxIndex = 3;
    if (Q[maxIndex] < 0) // ensure positive
        Q = -Q;
    float3 packed;
    if (maxIndex == 0)
        packed = Q.yzw();
    if (maxIndex == 1)
        packed = Q.xzw();
    if (maxIndex == 2)
        packed = Q.xyw();
    else /* maxIndex == 3 */
        packed = Q.xyz();
    packed *= sqrt(2.0f); // e.g. 45deg, max bounds
    packed = packed * 0.5f + 0.5f; // [-1,1] -> [0,1]
    return float4(packed, maxIndex / 3.0f);
}

// Unpacks quaternion from [UNORM XYZ, 2-bit max index] to quat
inline quat unpackQuaternionXYZPositionBit(float4 const& packed)
{
    uint maxIndex = packed.w * 3.0f;
    float3 p = packed.xyz() * 2.0f - 1.0f; // [0,1] -> [-1,1]
    p /= sqrt(2.0f);
    float4 Q;
    float maxValue = sqrt(max(.0f, 1 - p.x * p.x - p.y * p.y - p.z * p.z));
    if (maxIndex == 0)
        Q = float4(maxValue, p.xyz);
    else if (maxIndex == 1)
        Q = float4(p.x, maxValue, p.yz);
    else if (maxIndex == 2)
        Q = float4(p.xy, maxValue, p.z);
    else /* maxIndex == 3 */
        Q = float4(p.xyz, maxValue);
    return quat(Q.x, Q.y, Q.z, Q.w);
}

结合之前的定点量化和$RGB10A2$格式，我们能仅利用$4$字节做到完整的tangent frame存储。当然，还需要一个bit处理手性，故真正开销约莫为$33bits$

法向量 + 切向量旋转量

注： 此为真正使用的压缩方法

image-20251205173111991

idea来自RENDERING THE HELLSCAPE OF DOOM ETERNAL - SIGGRAPH 2020 —— 这里id只用了 $3$字节 来存储tangent frame！

不妨在法线所在平面内构造运行时某种正交基，因为我们的$\mathbf{t}$一定和他们共面：知道t和其中一个基底的夹角之后，用这两个向量基底构建就好。

这和四元数本身有异曲同工之妙——也是旋转轴+角度的表达。不过因为我们要的并非真正的四元数，这里没有对四个分量归一化的必要，精度分配上会自由很多。

Bitangent 符号

按 RENDERING THE HELLSCAPE OF DOOM ETERNAL - SIGGRAPH 2020 的做法，量化布局如下：

  • $2$字节存储八面体投影nomral
  • $1$字节存储tangent角度
  • 没了。

问题很显然：和四元数方法一样，我们丢掉了手性(bitangent)信息。Tangent Spaces and Diamond Encoding - jeremyong 在实现同样idea的评论到，或许丢掉也是一种解决方案。

However, I would contend that the above approach is better today for a few reasons:

  1. Not much content is mirrored anymore, since artists aren’t as memory constrained
  2. The extra draws aren’t relevant if you submit your draws as meshlets and GPU cull them anyways

In short, I recommend dropping the orientation bit altogether, given that times have changed in terms of how content is authored. As a compromise, it’s possible to store the orientation bit per-meshlet, or at some other frequency.

当然，这在mesh产生时就需要控制。遗憾地，对我们要读取的glTF格式而言，这并非一种选择。我们仍然需要存储这里的手性——之后会在packing过程选择一个量塞进去。

在线构造正交基

从法向量在线构造正交基的方法很多，参考：

最简单且快速的一种来自Building an Orthonormal Basis from a 3D Unit Vector Without Normalization - Frisvad, 2012，他在 UE 中也能见到。以下为简化实现：

inline void buildOrthonormalBasis(const float3 n, float3& b1, float3& b2)
{
    if (n.z < -0.9999999)
    {
        b1 = float3(0.0, -1.0, 0.0);
        b2 = float3(-1.0, 0.0, 0.0);
        return;
    }
    float a = 1.0 / (1.0 + n.z);
    float b = -n.x * n.y * a;
    b1 = float3(1.0 - n.x * n.x * a, b, -n.x);
    b2 = float3(b, 1.0 - n.y * n.y * a, -n.y);
}

不过，直接利用这些基底直接做bump map是不正确的——理由已在前文给出：法线贴图取决于烘焙到的tangent space，若要保持他们一致，则烘焙时和在线的结果也需一样：这很难做。但是知道多不正确，或者用他们如何重构$\mathbf{t}, \mathbf{b}$，则是很好做的一件事：$\mathbf{t}$投影算出夹角即可，手性计算和之前一致。

夹角：atan2 朴素实现

直接向两个正交基投影可得单位圆上对应坐标，实现如下。

float3 b1, b2;
buildOrthonormalBasis(normal, b1, b2);
// To angle
float cosAngle = dot(tangent, b1), sinAngle = dot(tangent, b2);
float angle = atan2(sinAngle, cosAngle) / pi<float>();
// From angle
tangent = cos(angle) * b1 + sin(angle) * b2;

注意这里存在atan2,cos,sin的使用。线代硬件跑这些函数“够快”——但是对值超大的输入会存在精度问题 然后能省的FLOP为啥不省 其次，实时渲染中几乎所有的操作都可以用不需要任何超越函数的方法实现：还请参阅iq大佬的 Avoiding trigonometry I，Avoiding trigonometry II，Avoiding trigonometry III 系列。

接下来介绍两个在此不需要三角函数的实现方法。

夹角：万能公式实现

别忘了高中学过的万能公式。特别地是以下三者（记$t = \tan \frac{\phi}{2} \newline$） $$ \cos \phi ={\frac {1-t^2}{1+t^2}} \newline \sin \phi ={\frac {2t}{1+t^2}} \newline \text{易得 } t={\frac {\sin \phi }{1+\cos \phi }}={\frac {\sin \phi (1-\cos \phi )}{(1+\cos \phi )(1-\cos \phi )}}={\frac {1-\cos \phi }{\sin \phi }} $$ 于是我们可以很轻松地得到不需要三角函数的实现，如下：

float3 b1, b2;
buildOrthonormalBasis(normal, b1, b2);
// To t
float cosAngle = dot(tangent, b1), sinAngle = dot(tangent, b2);
float t = sinAngle / (1 + cosAngle + EPS);
// From t
float cosAngle = (1 - t * t) / (1 + t * t + EPS), sinAngle = (2 * t) / (1 + t * t + EPS);
outTangent = cosAngle * b1 + sinAngle * b2;

不过问题也很显然：上面方法的$t$范围是全体实数——想要定点量化则是不可取的。

夹角：$L_1$投影

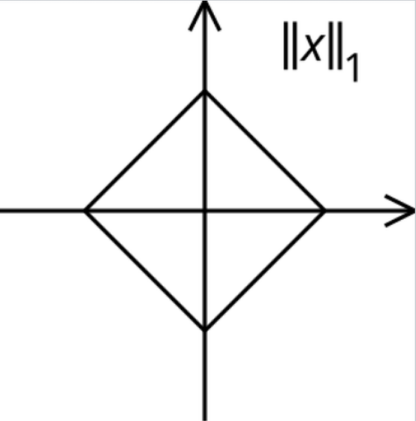
image-20251206094116091

其实，回顾之前的八面体投影——我们不妨给$\mathbb{R^2}$的单位圆做同样的事情：$\mathbf{L_1}$范式下的单位圆即上图。实现如下，和之前一样——我们将$\mathbf{L_1}$单位圆上的坐标投影到$x$轴上，不同的是这里符号直接代表$y$象限。

// R2, L2 to L1 projection on unit circle
float packUnitCircleSnorm(float2 v){
    v /= fabsf(v.x) + fabsf(v.y);
    return v.y >= EPS ? (v.x + 1.0f) * 0.5f : -(v.x + 1.0f) * 0.5f;
}
// R2, L1 to L2 projection on unit circle
float2 unpackUnitCircleSnorm(float v){
    float x = fabsf(v) * 2.0f - 1.0f;
    float y = 1.0f - fabsf(x);
    return normalize(v >= 0.0f ? float2(x, y) : float2(x, -y));
}

应用到tangent角度编码如下：

float3 b1, b2;
buildOrthonormalBasis(normal, b1, b2);
// To octAngle
float cosAngle = dot(tangent, b1), sinAngle = dot(tangent, b2);
float octAngle = packUnitCircleSnorm(float2(cosAngle, sinAngle));
// From octAngle
float2 octXY = unpackUnitCircleSnorm(octAngle);
outTangent = octXY.x * b1 + octXY.y * b2;

可见，编解码都很简单；且和之前一样，解码时仅仅涉及乘法加法：优势很明显。这将是我们用来存储夹角的方法。

最终量化

回顾我们一开始的完整vertex：

struct FVertex
{
    float3 position;
    float3 normal;
    float3 tangent;
    float bitangentSign;
    float2 uv;
};
static_assert(sizeof(FVertex) == 48);

结合前文所做的选择，以下是最终使用的量化后vertex结构：

struct FQVertex
{
    uint16_t position[4]; // quantized FP16 [xyz] padding [w]
    uint32_t tbn32; // packed tangent frame
    uint16_t uv[2]; // quantized FP16 [uv]

    static uint32_t PackTBN(const float3& normal, const float3& tangent, float bitangentSign);
    static void UnpackTBN(uint32_t packed, float3& outNormal, float3& outTangent, float& outBitangentSign);

    static FQVertex Pack(FVertex const& vertex);
    static FVertex Unpack(FQVertex const& vertex);
};
static_assert(sizeof(FQVertex) == 16);

  • position最后存在2字节的填充$w$。目的在于让最后整个vertex的大小为$4$的倍数（$16$）——meshoptmizer也会利用$4$对齐的属性提供一些操作（如下文提到的压缩）SIMD加速。此外，GPU也会更喜欢$4$对齐的数据：这点以后再提。

  • tbn32 即为tangent frame，这里使用了$4$字节存储与选择最后一种方案。bitfield格式如下：

    NormalX [12] NormalY [12] TangentAngle[7] BitangentSign[1]

    可见TBN是被完整存储的（包括手性bit）。多余的精度空间，我们把他放在了法向量packing上：24位专门用于normal，相对于四元数方法是个优势。

  • uv以UNORM FP16格式量化到$16+16$位存储。**注意：**虽然纹理本身空间是$[0,1]$，但UV本身是可以很大的，参考下图。

    image-20251208104343967

    这样可以达成tiling效果：开始写的时候还不知道 因为值域无界，这里只能使用正经的FP16。

最后：量化+压缩后的顶点格式是原大小的1/4 - 做的更好是有可能的：比如使用更低的顶点bit数处理TBN，这里就此折衷。此外，接下来实现光照部分时的GBuffer packing还将回顾这些手段。

以下为完整C++部分实现：

constexpr float EPS = 1e-6;
// Building an Orthonormal Basis from a 3D Unit Vector Without Normalization - Frisvad, 2012
// https://backend.orbit.dtu.dk/ws/portalfiles/portal/126824972/onb_frisvad_jgt2012_v2.pdf
inline void buildOrthonormalBasis(const float3 n, float3& b1, float3& b2)
{
    if (n.z < -0.9999999)
    {
        b1 = float3(0.0, -1.0, 0.0);
        b2 = float3(-1.0, 0.0, 0.0);
        return;
    }
    float a = 1.0 / (1.0 + n.z);
    float b = -n.x * n.y * a;
    b1 = float3(1.0 - n.x * n.x * a, b, -n.x);
    b2 = float3(b, 1.0 - n.y * n.y * a, -n.y);
}
// Original formulation from: https://jcgt.org/published/0003/02/01/paper.pdf
// R3, L2 to L1 projection on unit sphere
float2 packUnitOctahedralSnorm(float3 v)
{
    v /= float3(fabsf(v.x) + fabsf(v.y) + fabsf(v.z));
    return v.z >= EPS ? v.xy() : (float2(1.0f) - abs(float2(v.yx()))) * sign(float2(v.xy() + EPS));
}
// Original formulation from: https://jcgt.org/published/0003/02/01/paper.pdf
// R3, L1 to L2 projection on unit sphere
float3 unpackUnitOctahedralSnorm(float2 v)
{
    float3 nor = float3(v.xy(), 1.0f - fabsf(v.x) - fabsf(v.y));
    float2 xy = nor.z >= EPS ? v.xy() : (float2(1.0f) - abs(float2(v.yx()))) * sign(float2(v.xy() + EPS));
    return normalize(float3(xy.x, xy.y, nor.z));
}
// R2, L2 to L1 projection on unit circle
float packUnitCircleSnorm(float2 v){
    v /= fabsf(v.x) + fabsf(v.y);
    return v.y >= EPS ? (v.x + 1.0f) * 0.5f : -(v.x + 1.0f) * 0.5f;
}
// R2, L1 to L2 projection on unit circle
float2 unpackUnitCircleSnorm(float v){
    float x = fabsf(v) * 2.0f - 1.0f;
    float y = 1.0f - fabsf(x);
    return v >= 0.0f ? float2(x, y) : float2(x, -y);
}
// Compact TBN frame packing
// Tangent is derived from orthonormal basis around normal with a rotation angle
// Similar to 3 BYTE TANGENT FRAMES from "Rendering the Hellscape of Doom Eternal - SIGGRAPH 2020" by Jorge Jimenez et al.
// Octahedral normal [12+12] + tangent rotation [7] + bitangent sign [1]
// As a side effect - with tangent of length 0, a valid frame is still reconstructed
uint32_t FQVertex::PackTBN(const float3& normal, const float3& tangent, float bitangentSign)
{
    float3 b1, b2;
    buildOrthonormalBasis(normal, b1, b2);
    float cosAngle = dot(tangent, b1), sinAngle = dot(tangent, b2);
    float octAngle = packUnitCircleSnorm(float2(cosAngle, sinAngle));
    float2 oct = packUnitOctahedralSnorm(normal);
    uint32_t nX = quantizeSnormShifted(oct.x, 12), nY = quantizeSnormShifted(oct.y, 12);
    uint32_t tA = quantizeSnormShifted(octAngle, 7);
    uint32_t bS = bitangentSign >= 0.0f ? 1 : 0;
    uint32_t tbn32 = 0;
    tbn32 = bitfieldInsert(tbn32, nX, 0, 12);
    tbn32 = bitfieldInsert(tbn32, nY, 12, 12);
    tbn32 = bitfieldInsert(tbn32, tA, 24, 7);
    tbn32 = bitfieldInsert(tbn32, bS, 31, 1);
    return tbn32;
}
void FQVertex::UnpackTBN(uint32_t packed, float3& outNormal, float3& outTangent, float& outBitangentSign)
{
    uint32_t nX = bitfieldExtract(packed, 0, 12);
    uint32_t nY = bitfieldExtract(packed, 12, 12);
    uint32_t tA = bitfieldExtract(packed, 24, 7);
    uint32_t bS = bitfieldExtract(packed, 31, 1);
    float2 normalOct = float2(dequantizeSnormShifted(nX, 12), dequantizeSnormShifted(nY, 12));
    outNormal = unpackUnitOctahedralSnorm(normalOct);
    float octAngle = dequantizeSnormShifted(tA, 7);
    float2 octXY = unpackUnitCircleSnorm(octAngle);
    float3 b1, b2;
    buildOrthonormalBasis(outNormal, b1, b2);
    outTangent = octXY.x * b1 + octXY.y * b2;
    outBitangentSign = bS == 1 ? 1.0f : -1.0f;
}

网格压缩

在脱机存储上，局部量化以外，整体的数据压缩也是很有必要的。

通用压缩方案如LZ4以外，meshoptimizer 也提供了专用于顶点/index的压缩算法。使用还请参考原链接——在Editor场景序列化中，这些也是被使用到的。

效果

测试场景为Intel Sponza - 我们的格式仅保存几何数据。压缩前后磁盘存储大小如下。

mos9527@Sunrise:/mnt/Windows/Scenes » ls -altrh IntelSponza*.bin
-rwxrwxrwx 1 mos9527 mos9527 334M Nov 28 11:28 IntelSponzaOld.bin
-rwxrwxrwx 1 mos9527 mos9527 109M Dec  6 14:35 IntelSponza.bin

在GPU中上传后场景占用如下。

image-20251206144029344

References