Preface

After the v2 facial model update the game finally introduces SDF facial shadows; the implementation is pretty much the same as most of the existing solutions on the market.

This article shares one of my own ideas for correctly achieving this effect in Blender

Note: Due to personal limitations errors are inevitable, It is highly recommended to read the following text as a preparatory knowledge:

1. SDF Overview

SDF face shading offers considerable expressive freedom beyond addressing the shortcomings of plain normal/N dot L threshold shading for extreme light angle representations.

The implementation is also quite simple, here is an example of the application in HIFI Rush

Image source：Tango Gameworksのチャレンジが詰まったカートゥーン調リズムアクションゲーム『Hi-Fi RUSH（ハイファイラッシュ）』（1）キャラクター・モー*ション・エフェクト編

The art is based on the rendered output (with different light angles on the original geometry), which is hand-drawn as a threshold map based on angles and then subjected to some kind of compositing algorithm to generate an SDF image with luminance mapped to the light angles.

Shading-wise, SDF can convert the problem of Point/Fragment rendering to Object/Object overall rendering

The final coloring is related and only related to the lighting angle (knock on wood), which is somehow equivalent to shading a plane that is normal to the same line

Synthesized, there’s Valve on Technical Sharing at SIGGRAPH 2007 and quite a few tutorials will introduce the 8-points Signed Sequential Euclidean Distance Transform/8SSEDT
Both will be realized and dissected in more depth in subsequent articles

Of course, this post is still focused on reproducing the game’s effects

2. In-game implementation

The SDF mapping used for the extraction game is as follows

faceSdf

Viewing the threshold in Photoshop, it’s clear that it’s a similar model to the one described above

Recall that the threshold we need **corresponds to the light angle; which will be used right away next (again, knock on wood)

3. Blender implementation

Illumination angle

From the perspective, consider a single light vector $l$ – as in the figure (from RTR4 … Of course there is no direct connection to the BRDF here

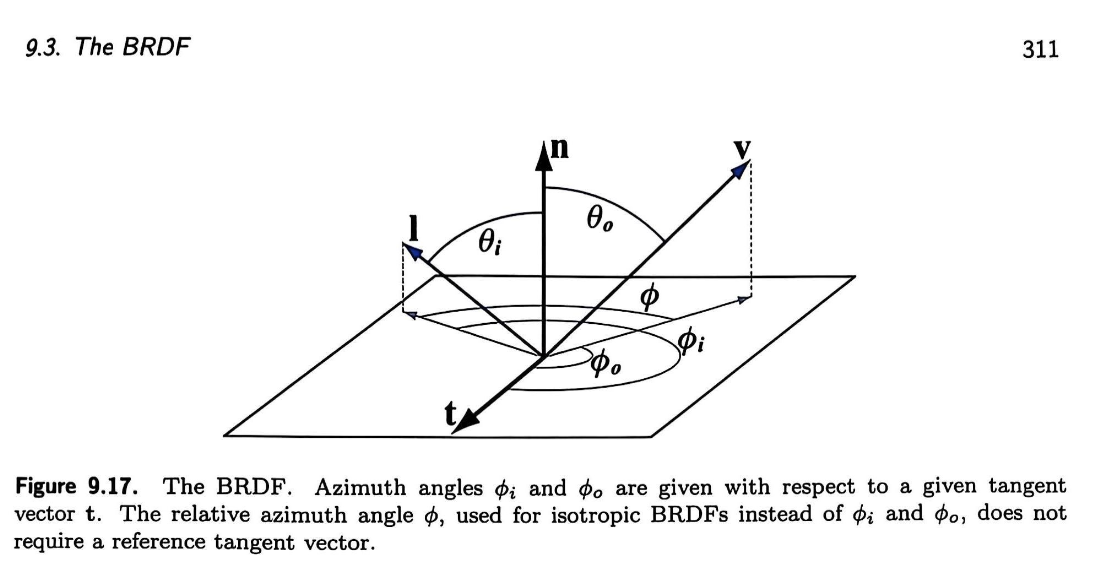
Because of the symmetry it is clear that with only $ \mathbf{\hat{n}}} \cdot \mathbf{\hat{l}}$ we can only obtain $\theta \in [0,90\degree]$ the angle of illumination (the $<0$ part of the backlighting is therefore omitted).

However, the introduction of tangent vectors can solve the problem! This will allow us to observe the light vectors in spherical coordinates

Only view vectors $n$ and tangent vectors $t$ are taken into account, without considering viewpoints $v$.

Obviously there are $cos\theta_i = n \cdot l, cos\phi_i = t \cdot l$
Recalling the previous $\theta$ range, note that $\phi \leq 180\degree$ corresponds to the half-space on the $b = n \times t$ side, and vice versa!
As above, combining the symmetry, the light angle of $[-90\degree,90\degree]$ can be easily obtained according to $\phi$
The formula is as follows, noting $\omega$ as the final light angle $$ \omega = \theta_i * sgn(sin \phi_i) $$

Tangent space perspective

Note: In fact, there is no need to write = = = The relationship between the $\theta$ angle and $N$ should be obvious as $cos\theta= \mathbf{L \cdot N}$.

The use of the cut space /$\mathbf{TBN}$ representation is presented next

First of all it is known from above that we already have the orthogonal basis $\mathbf{t,b,n}$ ($b$ is the $t,n$ fork product) and the $\mathbf{TBN}$ matrix is as follows $$ \mathbf{TBN} = \begin{bmatrix} T_0 & B_0 & N_0 \newline T_1 & B_1 & N_1 \newline T_2 & B_2 & N_2 \end{bmatrix}. $$ Clearly, $\mathbf{TBN}$ is an orthogonal matrix, implying that its transpose is equal to its inverse $$ \mathbf{TBN}^\top = \mathbf{TBN}^{-1} = \begin{bmatrix} T_0 & B_0 & N_0 \newline T_1 & B_1 & N_1 \newline T_2 & B_2 & N_2 \end{bmatrix}. $$

Next do a linear space transformation to put the light vector $\mathbf{L}$ into tangent space: $$ \mathbf{L} = [x_0,y_0,z_0]^T = a\mathbf{T}+b\mathbf{B}+c\mathbf{N} $$

$$ \begin{bmatrix} a \newline b \newline c \end{bmatrix} = \mathbf{TBN}^{-1} \begin{bmatrix} x_0 \newline y_0 \newline z_0 \end{bmatrix} = \mathbf{TBN}^\top \begin{bmatrix} x_0 \newline y_0 \newline z_0 \end{bmatrix} $$

$$ \left\lbrace\begin{array}{clcr} a = T_0 x_0 + T_1 y_0 + T_2 z_0 = \mathbf{L \cdot T} \newline b = B_0 x_0 + B_1 y_0 + B_2 z_0 = \mathbf{L \cdot B} \newline c = N_0 x_0 + N_1 y_0 + N_2 z_0 = \mathbf{L \cdot N} \end{array} \right. $$

The projection of $L$ in the plane where $\mathbf{t}$ is located has

$$ \mathbf{L_bn} = b\mathbf{B}+c\mathbf{N} = \mathbf{L} - a\mathbf{T} $$

To find $\theta$ is to say that

$$ cos\theta=\mathbf{L_{bn} \cdot N} = \mathbf{L \cdot N} $$

Identically related

$$ cos\phi = \mathbf{L \cdot T} $$

Tangent space construction (math.)

Many tutorials on implementing SDF in Blender make the assumption that the normal vector of the coloring plane is the +Y axis, e.g. setting up the Driver to take the azimuth directly from Euler Z, which points to the light.

The problem is obvious; here’s a way to implement the trick in Blender without compromising accuracy.

Driver

Considering that the animation will take place on the skeleton, here we consider taking the normal vector directly on the skeleton.

Game character models consistently have a Head bone, which can be used later; for the sake of convenience, some of these will be demonstrated later using a simplified model.

Similar to the previous idea of taking edge highlights, the Euler XYZ of World Space is taken directly to compute the normal vector corresponding to the bones.

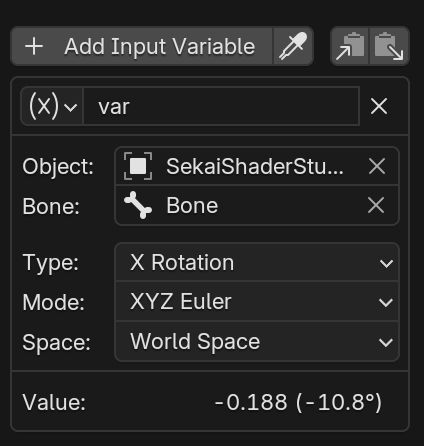
One of the many benefits of World Space is that the algorithm for this value includes animation (FCurve), Constraints and Parenting - even for bones!

The effect is as follows：

Tectonic orthogonal basis (math.)

Of course, so we don’t have the tangent vector $t$ yet; fortunately it is not difficult to construct orthogonal bases from normal vectors.

The following code blocks are taken from the referenced paper Building an Orthonormal Basis from a 3D Unit Vector Without Normalization - Frisvad, Jeppe Revall

The plain idea is simple: pick an axis closer to the normal vector, orthogonalize it, and do a cross-multiplication to get an $n,t,b$ orthogonal basis

void naive ( const Vec3f & n , Vec3f & b1 , Vec3f & b2 )
{
  // If n is near the x-axis , use the y- axis . Otherwise use the x- axis .
  if(n.x > 0.9 f ) b1 = Vec3f (0.0f , 1.0f , 0.0f );
  else b1 = Vec3f (1.0f , 0.0f , 0.0f );
  b1 -= n* dot (b1 , n ); // Make b1 orthogonal to n
  b1 *= rsqrt ( dot (b1 , b1 )); // Normalize b1
  b2 = cross (n , b1 ); // Construct b2 using a cross product
}

This approach intuitively fits our requirement for $t$-vectors: one can decide which side of $b = n \times t$ the light vector is on

And the construction method given in the paper is quite beautiful

void frisvad ( const Vec3f & n , Vec3f & b1 , Vec3f & b2 )
{
if(n.z < -0.9999999 f) // Handle the singularity
{
  b1 = Vec3f ( 0.0f , -1.0f , 0.0f );
  b2 = Vec3f ( -1.0f , 0.0f , 0.0f );
  return ;
  }
  const float a = 1.0 f /(1.0 f + n.z );
  const float b = -n.x*n .y*a ;
  b1 = Vec3f (1.0 f - n .x*n. x*a , b , -n .x );
  b2 = Vec3f (b , 1.0 f - n .y*n. y*a , -n .y );
}

It can be seen that we don’t need fork multiplication and don’t need normalization to get two extra bases

Space (and level) is limited here do not do not introduce, interested also refer to the original understanding

The next step is easy to implement in Blender using Shader Node (note: this ignores the case where the normal is at the z-axis cutoff point).

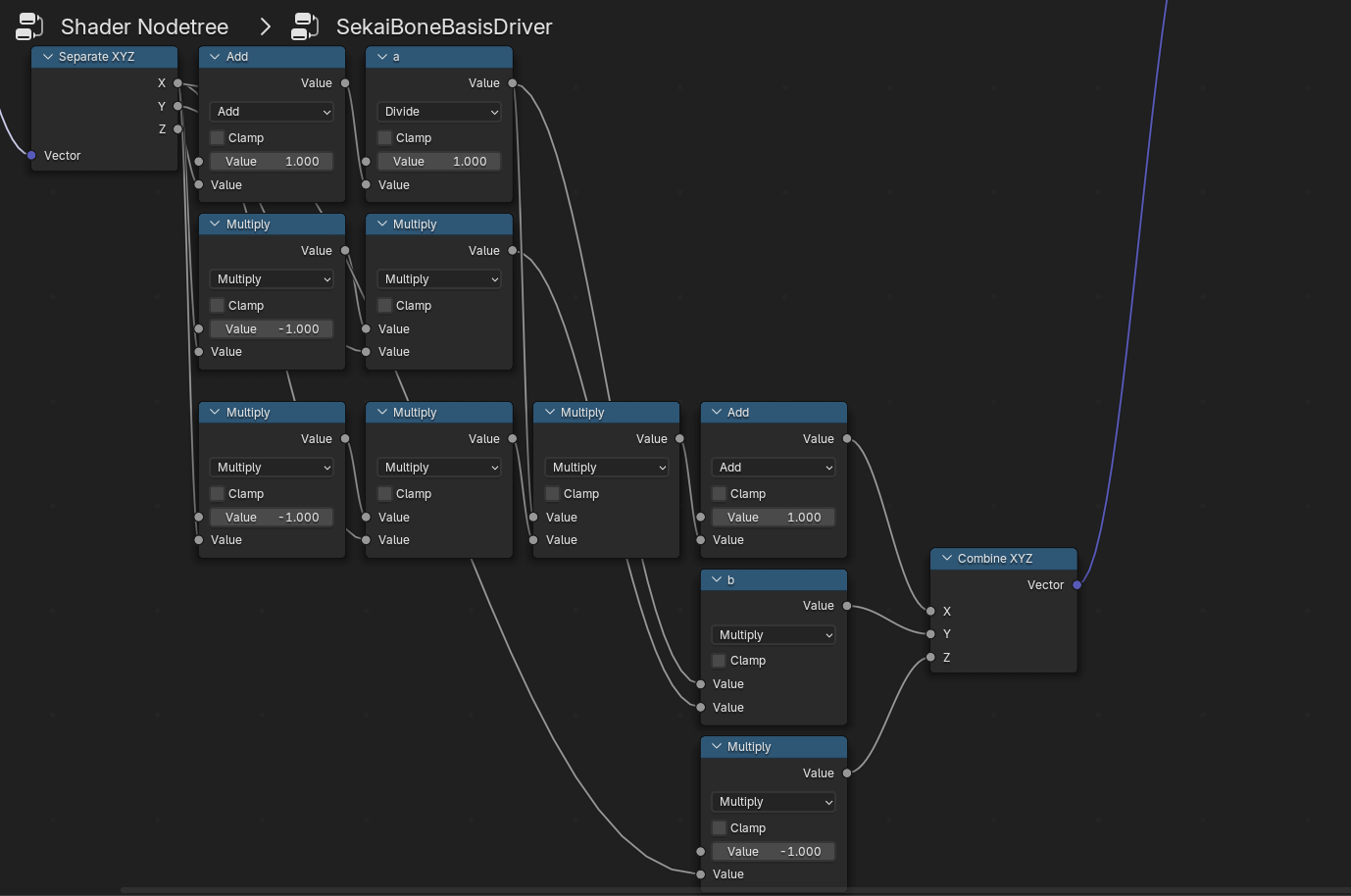
Organizational realizations

Using $cos \phi, cos \theta$ from above, it’s a snap to realize that

Material handling

For one thing, since the in-game material only takes into account the horizontal angle of the lighting scheme, it is necessary to drop the $z$-axis calculation when calculating the $\theta$ angle; otherwise the angular difference brought about by this angle will only bring about an error.
- See the link at the top of the article for the program with vertical corners, which will not be presented at this time.
Second, the mapping only contains information about horizontal angles in $[0,90\degree]$; meaning that beyond that range (in $[-90\degree,0]$) you need to borrow the symmetry inversion.
- The resulting face model also needs to be symmetrical; of course, making two SDF maps wouldn’t have this limitation.

Node is as follows

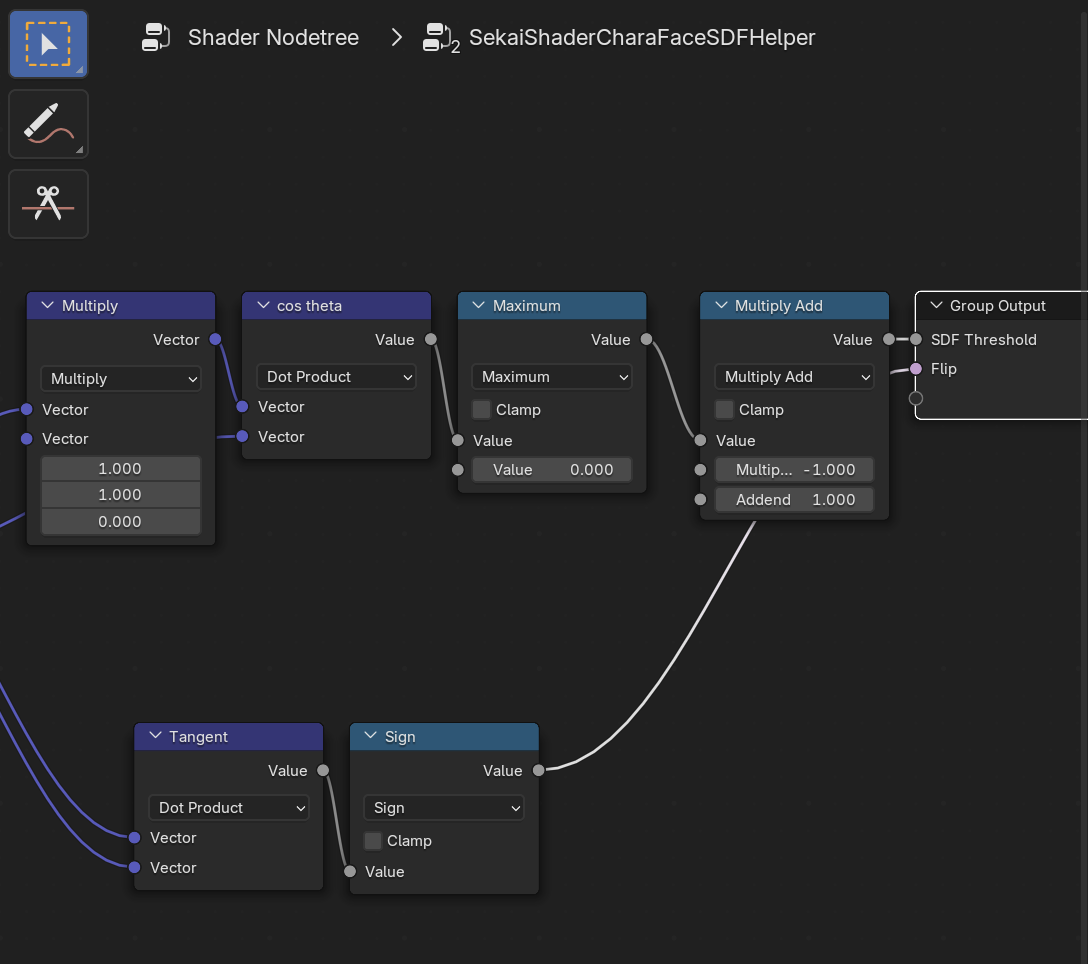
The Node used for inversion is as follows

The inversion is simply $u = 1 - u$

Final result

The effect is practiced in the animation as follows; you can see that the threshold lighting also changes correctly in the bone movements.

PSJK Blender Cartoon Render Pipeline Revisited【3】- SDF face rendering implementation

Preface

1. SDF Overview

2. In-game implementation